第5章 協調ベース推薦システム~モデルベース協調フィルタリング~
第5章 協調ベース推薦システム~モデルベース協調フィルタリング~
表5.aはユーザ-焼肉評価値行列である。各行はユーザ\(u\)を、各列はアイテム\(i\)を表す。行列の\((u, i)\)成分は、ユーザ\(u\)がアイテム\(i\)に与えた評価値\(r_{u,i} \in \{-1, +1\}\)を表す。ただし、\(?\)となっている成分は欠損値であることを表す。このとき、次の問いに答えなさい。
表5.a ユーザ-焼肉評価値行列
| カルビ $(i=1)$ | ハラミ $(i=2)$ | ロース $(i=3)$ | タン $(i=4)$ | |
|---|---|---|---|---|
| Alice $(u=1)$ | +1 | -1 | ? | ? |
| Bruno $(u=2)$ | +1 | -1 | ? | +1 |
| Chiara $(u=3)$ | +1 | -1 | -1 | +1 |
| Dhruv $(u=4)$ | ? | -1 | -1 | -1 |
| Emi $(u=5)$ | +1 | ? | -1 | -1 |
| Faye $(u=6)$ | -1 | -1 | +1 | -1 |
| Gilles $(u=7)$ | -1 | +1 | -1 | ? |
1. ルールベース協調フィルタリング
演習問題1
次の各ルールの出現頻度を求めなさい。
(1) ルール\(\{\text{カルビ} = +1\} \Rightarrow \text{ロース} = -1\)
(2) ルール\(\{\text{カルビ} = +1, \text{ハラミ} = -1\} \Rightarrow \text{ロース} = -1\)
(3) ルール\(\{\text{ハラミ} = -1, \text{タン} = -1, \text{カルビ} = -1\} \Rightarrow \text{ロース} = +1\)
演習問題2
次の各ルールの支持度を求めなさい。
(1) ルール\(\{\text{カルビ} = +1\} \Rightarrow \text{ロース} = -1\)
(2) ルール\(\{\text{カルビ} = +1, \text{ハラミ} = -1\} \Rightarrow \text{ロース} = -1\)
(3) ルール\(\{\text{ハラミ} = -1, \text{タン} = -1, \text{カルビ} = -1\} \Rightarrow \text{ロース} = +1\)
演習問題3
次の各ルールの確信度を求めなさい。
(1) ルール\(\{\text{カルビ} = +1\} \Rightarrow \text{ロース} = -1\)
(2) ルール\(\{\text{カルビ} = +1, \text{ハラミ} = -1\} \Rightarrow \text{ロース} = -1\)
(3) ルール\(\{\text{ハラミ} = -1, \text{タン} = -1, \text{カルビ} = -1\} \Rightarrow \text{ロース} = +1\)
演習問題4
最小支持度を\(\mathit{minsup} = 0.2\)、最小確信度を\(\mathit{minconf} = 0.5\)とするとき、ロースの好き嫌いに関する相関ルールをすべて挙げなさい。
演習問題5
Brunoのロースに対する予測評価値を求めなさい。ただし、確信度による重みは考慮しない。
2. 単純ベイズ協調フィルタリング
演習問題6
事前確率として、ロースを好む確率および嫌う確率をそれぞれ求めなさい。ただし、ラプラススムージングは適用しない。答は分数のままでよい。
演習問題7
表5.bは単純ベイズ協調フィルタリングによるロースに関する学習モデルである。アイテムごとの条件付き確率を求め、表5.bの学習モデルを完成させなさい。ただし、ラプラススムージングは適用しない。各確率は分数のままでよい。
表5.b 単純ベイズ協調フィルタリングによるロースに関する学習モデル
| 事前確率 | カルビ | ハラミ | ロース | タン | |||||
|---|---|---|---|---|---|---|---|---|---|
| 好き | 嫌い | 好き | 嫌い | 好き | 嫌い | 好き | 嫌い | ||
| 好き | 演習問題6 | (1) | (2) | 0/1 | 1/1 | - | - | 0/1 | 1/1 |
| 嫌い | 演習問題6 | (3) | (4) | 1/3 | 2/3 | - | - | 1/3 | 2/3 |
演習問題8
ラプラススムージングを適用したとき、事前確率として、ロースを好む確率および嫌う確率をそれぞれ求めなさい。ただし、スムージングパラメタは\(\alpha = 1\)とする。また、答は分数のままでよい。
演習問題9
表5.cはラプラススムージングを適用した単純ベイズ協調フィルタリングによるロースに関する学習モデルである。ラプラススムージングを適用したとき、アイテムごとの条件付き確率を求め、表5.cの学習モデルを完成させなさい。ただし、スムージングパラメタは\(\alpha = 1\)とする。また、各確率は分数のままでよい。
表5.c ラプラススムージングを適用した単純ベイズ協調フィルタリングによるロースに関する学習モデル
| 事前確率 | カルビ | ハラミ | ロース | タン | |||||
|---|---|---|---|---|---|---|---|---|---|
| 好き | 嫌い | 好き | 嫌い | 好き | 嫌い | 好き | 嫌い | ||
| 好き | 演習問題8 | (1) | (2) | 1/3 | 2/3 | - | - | 1/3 | 2/3 |
| 嫌い | 演習問題8 | (3) | (4) | 2/5 | 3/5 | - | - | 2/5 | 3/5 |
演習問題10
ラプラススムージングを適用したとき、Brunoがロースを好む確率および嫌う確率をそれぞれ求めなさい。ただし、スムージングパラメタは\(\alpha = 1\)とする。
演習問題11
ラプラススムージングを適用したとき、Brunoのロースに対する予測評価値を求めなさい。ただし、スムージングパラメタは\(\alpha = 1\)とする。
3. 決定木に基づく協調フィルタリング
ロース用の決定木を学習することを考える。表5.dはロースに対する評価値を目的変数とした次元削減後の評価値行列である。各行はユーザ\(u\)を表す。\(p_{u,1}, p_{u,2}\)は潜在因子を表し、説明変数に対応する。\(r_{u,3} \in \{-1, +1\}\)はユーザ\(u\)がロースに与えた評価値を表し、目的変数に対応する。ただし、\(?\)となっている成分は欠損値であることを表す。このとき、次の問いに答えなさい。
表5.d ロースに対する評価値を目的変数とした次元削減後の評価値行列
| \(p_{u,1}\) | \(p_{u,2}\) | \(r_{u,3}\) | |
|---|---|---|---|
| Alice $(u=1)$ | -0.533 | -0.465 | ? |
| Bruno $(u=2)$ | -0.559 | -0.076 | ? |
| Chiara $(u=3)$ | -0.559 | -0.076 | -1 |
| Dhruv $(u=4)$ | 0.125 | -0.679 | -1 |
| Emi $(u=5)$ | -0.044 | -0.489 | -1 |
| Faye $(u=6)$ | 0.317 | -0.361 | 1 |
| Gilles $(u=7)$ | 0.533 | 0.465 | -1 |
演習問題12
ロース用の訓練データ\(D_{3}^{L}\)を、\(p_{u,1} \leq 0.221\)の事例集合\(D_{3}^{L0}\)と、 \(p_{u,1} > 0.221\)の事例集合\(D_{3}^{L1}\)に分割したとする。このとき、それぞれのジニ係数\(G(D_{3}^{L0})\)、\(G(D_{3}^{L1})\)を求めなさい。
演習問題13
ロース用の訓練データ\(D_{3}^{L}\)を、それぞれ次の基準で分割したとき、その分割のよさをジニ係数の加重平均により求めなさい。
(1) \(p_{u,1} \leq 0.221\)の事例集合\(D_{3}^{L0}\)と、 \(p_{u,1} > 0.221\)の事例集合\(D_{3}^{L1}\)
(2) \(p_{u,2} \leq -0.425\)の事例集合\(D_{3}^{L0}\)と、 \(p_{u,2} > -0.425\)の事例集合\(D_{3}^{L1}\)
演習問題14
潜在因子\(p_{u,1}, p_{u,2}\)について、選択基準の候補として、\(p_{u,1} = \{-0.302, 0.040, 0.221, 0.425\}\)、\(p_{u,2} = \{-0.584, -0.425, -0.218, 0.195\}\)を考える。このとき、レベル0の選択基準として適切な属性を挙げなさい。
演習問題15
ロース用の学習モデルとして図5.aの決定木が構成されたとする。このとき、次の各予測評価値を求めなさい。
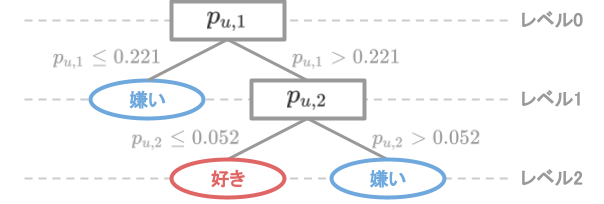
図5.a ロース用の決定木